Curve Skeletonization in Continuous domain for Meshes and Point Clouds
Abstract
Advancements in 3D curve skeletonization are accelerating progress across a wide range of applications. However, developing robust skeletonization algorithms that capture intricate object details remains challenging. Skeletonization via Local Separators (LS) offers an efficient graph-based approach but suffers from representation inaccuracies due to its discrete nature. To address this, we introduce CSCD, a novel framework for Curve Skeletonization in the Continuous Domain, generalizing LS to manifolds. Specifically, we present two realizations: CSCD-M for meshes and CSCD-PC for point clouds. \cscd-M leverages the intrinsic triangulation of a mesh for resilience to noise and improved topological preservation, while CSCD-PC employs tufted Laplacians for enhanced robustness. To our knowledge, CSCD-M is the first intrinsic method for curve skeletonization. Our results show CSCD-M matches LS performance across diverse meshes and outperforms LS (TOG'21) on benchmarks like Thingi10k dataset. CSCD-PC qualitatively outperforms CoverageAxis++ (Eurographics'24) and EPCS (CAG'23). Finally, we demonstrate the efficacy of CSCD in a few downstream tasks: object classification, shape segmentation, identifying handles, tunnels, and constrictions in objects.
Approach
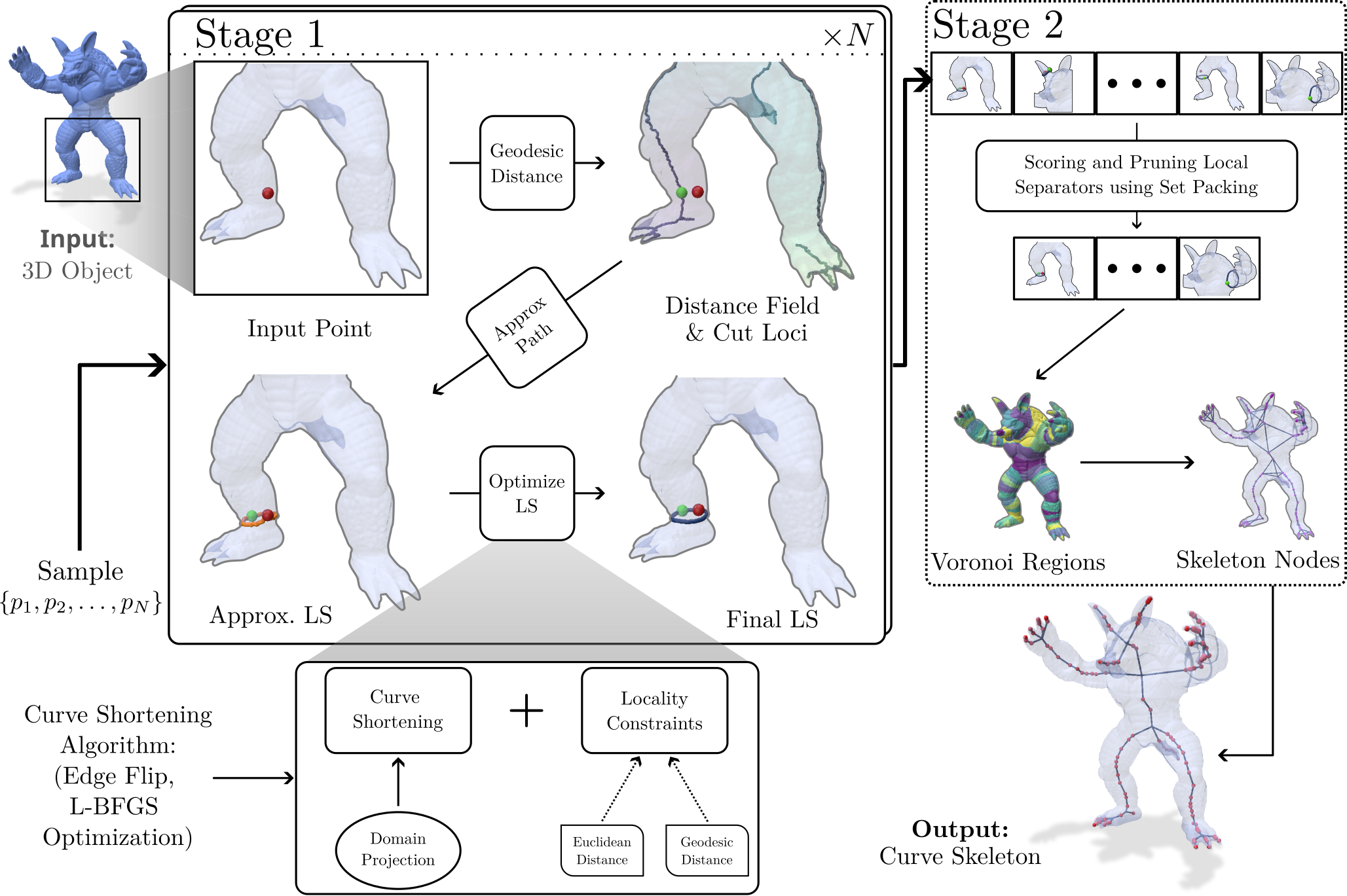
The entire Curve Skeletonization framework can be divided into two stages. In Stage 1, we calculate the various local separators given the 3D object as input(input can be a mesh or a point cloud). Once we have a sampled point, we calculate the geodesic distance to all other points and find the cut loci of the point to identify the target cut locus. Then an approximate local separator (LS) is constructed, followed by the LS optimization. The optimization is specific to the particular representation and is in the presence of a locality constraint. In Stage 2, we calculate the skeleton from the set of local separators. First, we prune and pack the previously obtained separators. Based on the obtained separators, we divide the object into Voronoi regions. These regions correspond to nodes, and neighbouring regions are connected to give the skeleton. Post-processing is finally performed to convert cliques to stars in the resultant skeleton.
Results
Results on Meshes
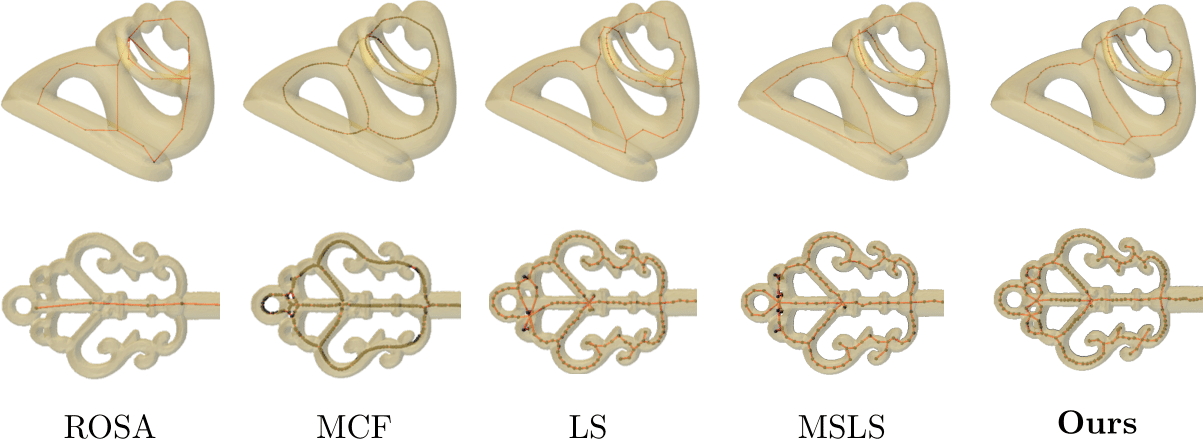
Qualitative results of our method: ROSA struggles to capture mesh details, while MCF produces overly smooth skeletons. CSCD-M, LS and MSLS yield comparable results on meshes; however, our method correctly captures details, as seen on the copper key. In fertility, our approach results in smoother skeletons compared to LS and MSLS.
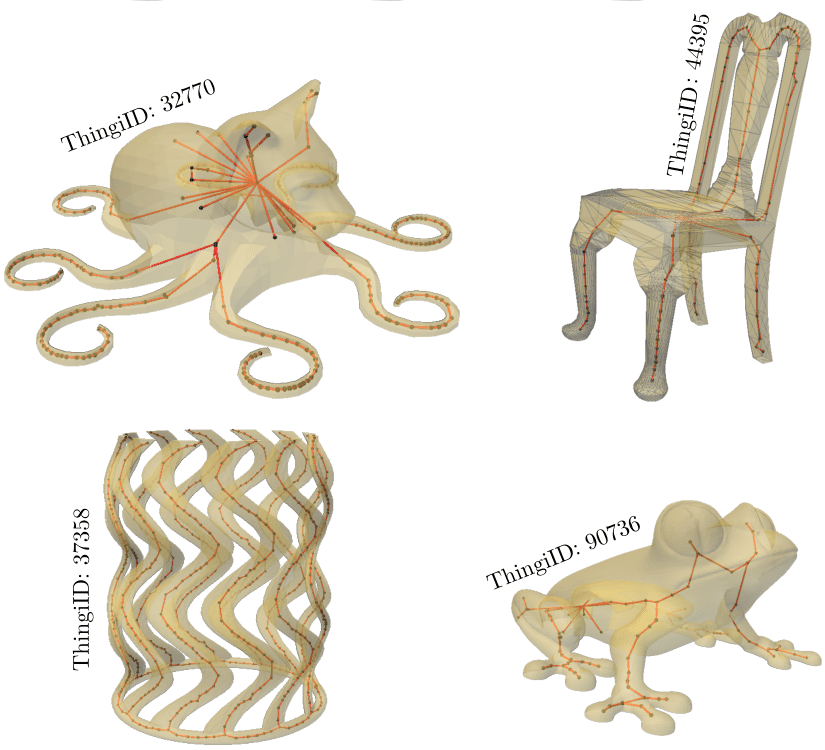
Qualitative results of CSCD-M on Thingi10k. CSCD-M performs well even on poorly triangulated meshes.

CSCD-M and MSLS on a torus with holes. Left panel, CSCD-M local separators on the torus -- highlighting how the separators go around the holes. Right panel, comparison of the curve skeleton obtained by MSLS and Ours (CSCD-M).
Results on Point Clouds
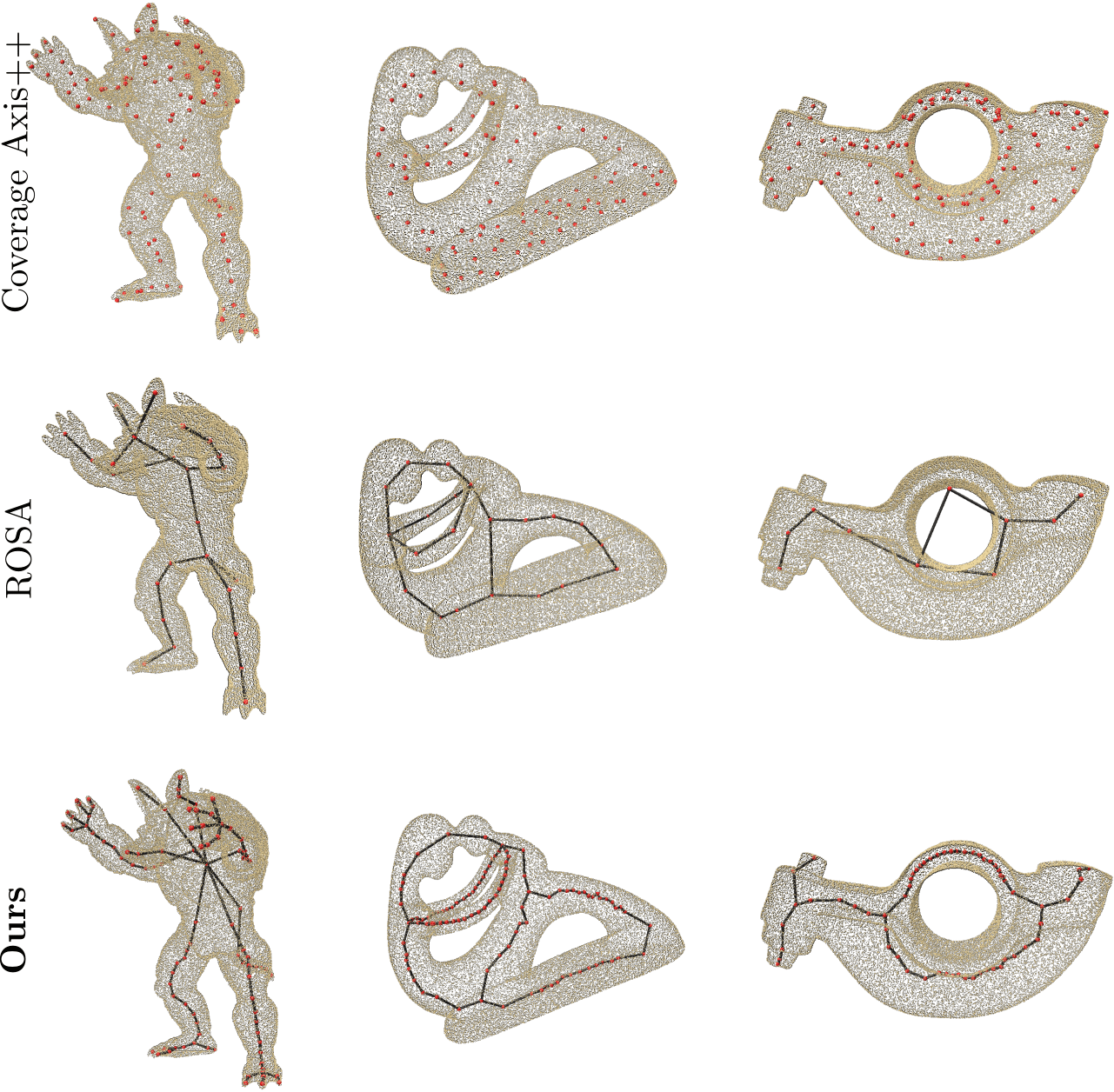
CSCD-PC vs ROSA vs CA++ [Eurographics'24]: CA++ fails to generate a valid skeleton (since it's a MAT inspired algorithm). Our method captures object details better, yielding more nodes and centered skeletons compared to ROSA.
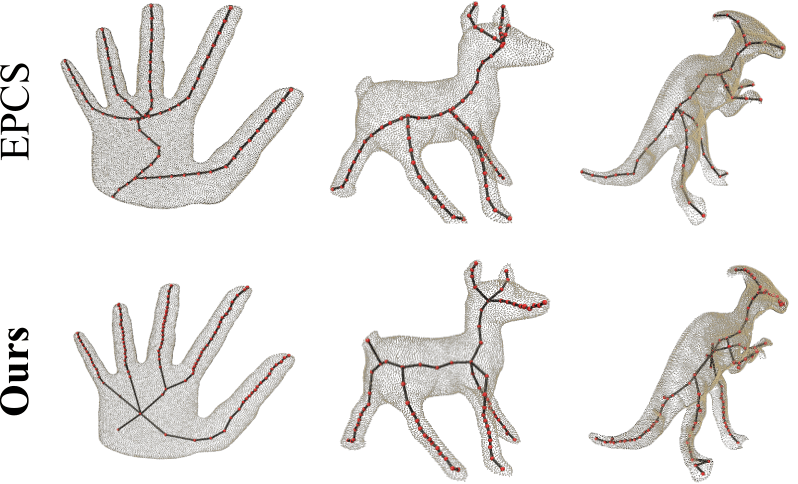
CSCD-PC vs EPCS [CAG'23]: Our method captures object details better, compared to EPCS. In hand (left), our skeleton is centered indd the palm and shows skeleton consistent with square shape. In deer (middle), we capture the snout and the tail. In dino (right), EPCS fails to capture the curvature of the arm completely while our skeleton follows the arm.
BibTeX
@article{cscd,
title={Curve Skeletonization in Continuous domain for Meshes and Point Clouds},
author={Anonymous},
journal={Conference/Journal Name},
year={2025},
url={https://cscd-skel.pages.dev},
}